Rayleigh-Rice Mixture Model Estimation

Problem in hand

Consider the data with all positive values denoted as $s_n$ for all $n\in\{1,\cdots,N\}$. It is desired to find an unsupervised threshold $\tau_s$ such that we say for $s_n>\tau_s$ the data point $n$ belongs to a class otherwise the data point belongs to the other class. In order to find such a threshold without introducing any extra parameters we use a Rayleigh-Rice mixture model. Note that the values of $s_n$ are positive and Rayleigh-Rice mixture models these values very well. Once the Rayleigh-Rice mixture model is fitted, the intersection of the two distributions is the threshold value.

Rayleigh-Rice mixture

Let $\alpha$ indicate the probability that a sample $s$ is from a Rayleigh distribution with parameter $b^2$ and $1-\alpha$ the probability that $s$ is from the Rice distribution with parameters $\nu$ and $\sigma^2$. Then, the distribution of the mixture model can be written as

where $\Psi = \{\alpha, b^2, \nu, \sigma^2\}$ and

and

with $I_0(\cdot)$ is the 0-th order modified Bessel function of first kind. Given the samples $\{s_n\}_{n=1}^N$ we want to find the parameters of this model ($\Psi = \{\alpha, b^2, \nu, \sigma^2\}$). Expectation-Maximization (EM) algorithm can be used to estimate the model parameters $\Psi$. Following algorithm shows the steps of the EM for fitting the Rayleigh-Rice model.

Given the fitted model parameters the threshold value is found by solving the following for $\tau_s$.

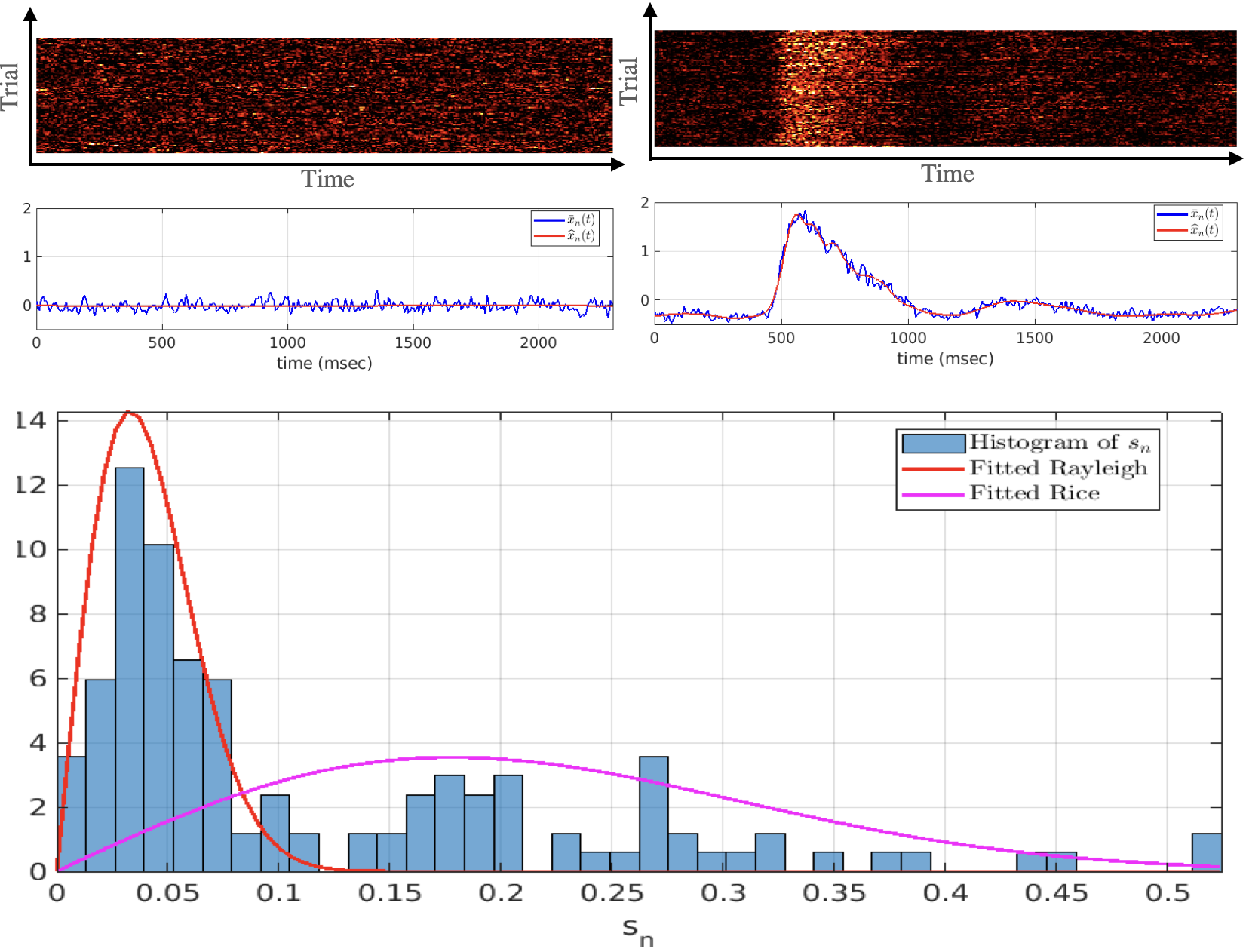
Sample Result

A sample histogram of $s_n$ for all $n\in\{1,\cdots,N\}$ is shown in figure. The plotted curves show the fitted Rayleigh and Rice distributions. In this example, the values of $s_n$ denote the standard deviation of electrode activity and the fitted model separates the active and inactive electrodes.

Matlab implementation

The matlab implementation is provided here.