Overlaying Model for Video Foreground-Background Subtraction
Abstract
Moving object detection in a given video sequence is a pivotal step in many computer vision applications such as video surveillance. Robust Principal Component Analysis (RPCA) performs low-rank and sparse decomposition to accomplish such a task. A fundamental issue with the RPCA is the assumption that the low-rank and sparse components are added at each pixel, whereas in reality, the moving foreground is overlaid on the background. We propose the masked decomposition (i.e. an overlaying model) where each element either belongs to the low-rank or the sparse component, decided by a mask. We introduce the Masked-RPCA (MRPCA) algorithm to recover the mask (hence the sparse object) and the low-rank components simultaneously, via a non-convex formulation. An adapted version of the Douglas–Rachford splitting algorithm is utilized to solve the proposed formulation.
Additive model
Let us consider the matrix constructed by vectorizing the video frames of size in to -vectors and stacking them as columns of the matrix . Robust Principal Component Analysis (RPCA) attempts to efficiently find matrices and such that with as the low-rank and as the sparse component.The foreground-background subtraction via RPCA model can be achieved by solving the convex optimization problem as
with variables and , where denotes the nuclear norm (sum of singular values), denotes the sum of absolute value of the entries (not the -norm in the matrix sense), and is a regularization parameter. This formulation is also known as principal component pursuit (PCP) method in the literature and can be solved by utilizing the augmented Lagrange multiplier (ALM) method. 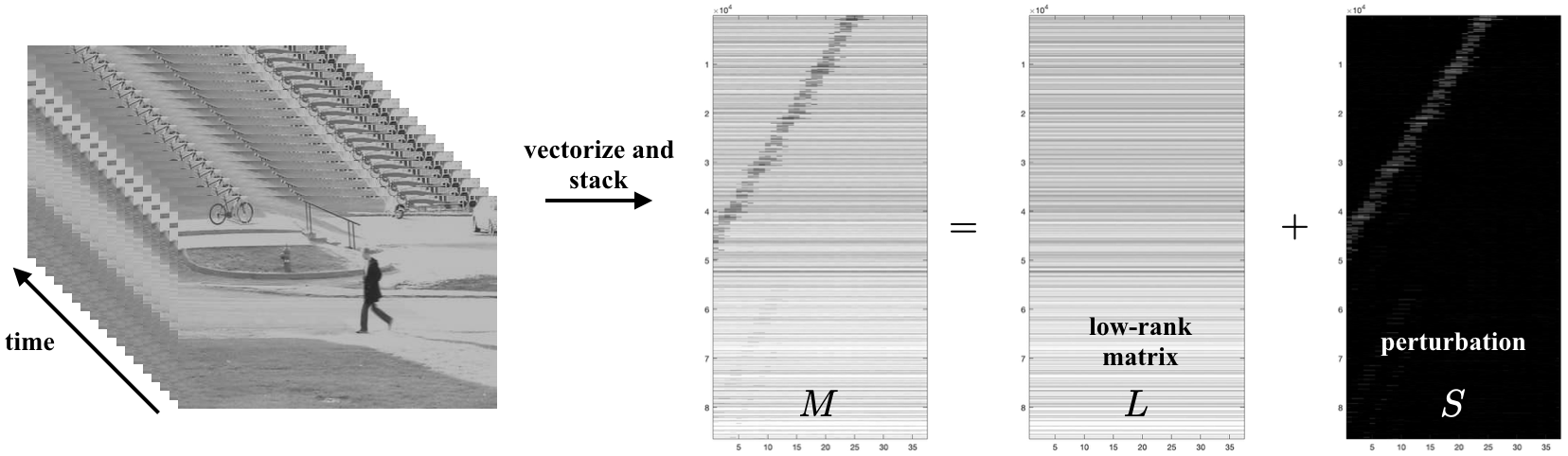

Overlaying model
Additive perturbation is not a realistic assumption in video foreground-background decomposition. One immediate consequence of the additive model is that the recovered foreground object would not have the correct color. We forgo the additive assumption and instead propose a formulation of an overlaying model, which acknowledges that the foreground object is overlaid on top of the background and is occluding it (rather than simply being added).
The goal is to find matrices (with low-rank structure) and (with sparse structure) such that the overlaying model is satisfied. A plausible formulation of such problem can be written as
where is a regularization parameter and is a penalty parameter. The indicator function ensures . The algorithm to solve this problem is not immediately obvious. The details of how this probelm is solved can be found in the related paper.
Sample results
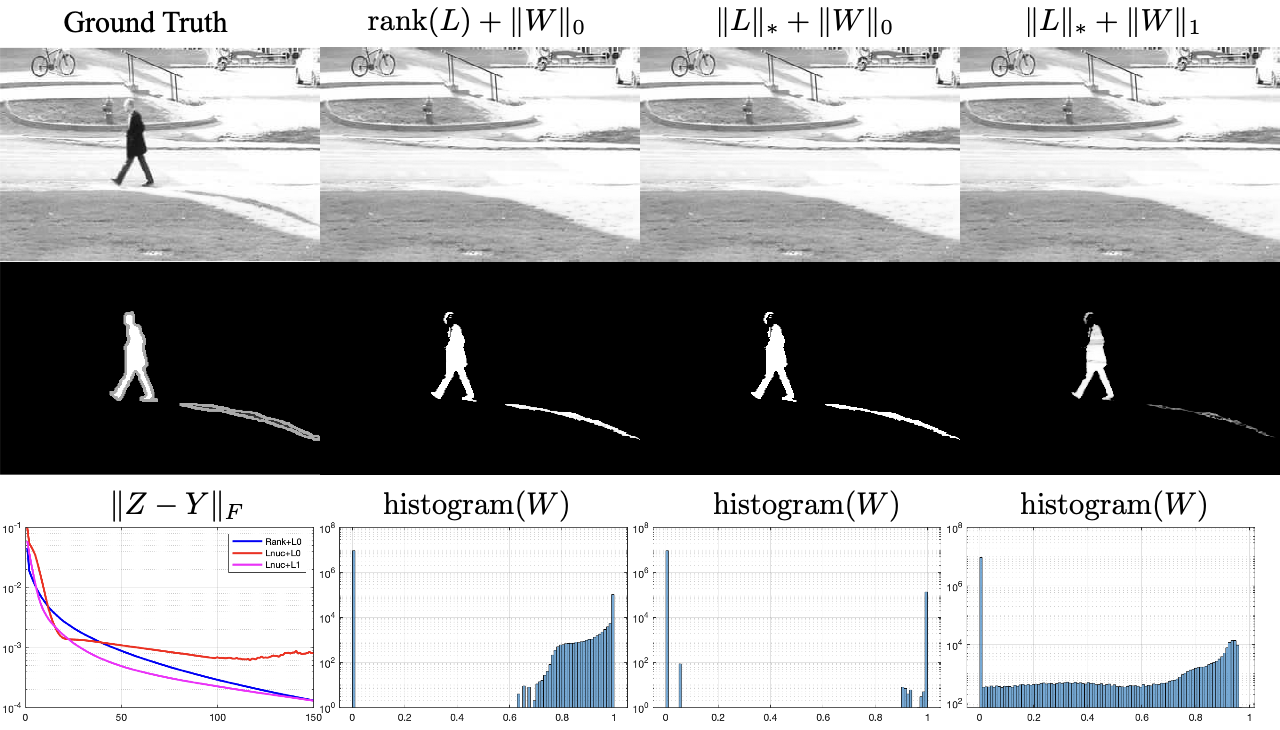
A frame of the resulting background and mask for different variants of the overlaying model are shown in this figure. Additionally, last row shows the duality gap between the split variables and is an indicator for the convergence of the algorithm showing that all proposed methods converge within few tens of iterations. Histogram of the recovered mask for all different methods is shown in following figure. As we can observe, the non-convex priors lead to a separation of the values.
Matlab implementation
The matlab implementation is provided here.
Related publications
A. Khalilian-Gourtani, S. Minaee, and Y. Wang. "Masked-RPCA: Moving Object Detection with an Overlaying Model", IEEE Open Journal of Signal Processing, vol. 1, 2020. pdf
A. Khalilian-Gourtani, S. Minaee, and Y. Wang. "Masked-RPCA: Sparse and low-rank decomposition under overlaying model and application to moving object detection." arXiv preprint, 2019. pdf